1536. Любимый ребенок мешает
Дети всегда
любимые, но иногда они могут заставить Вас вести себя резко. В этой задаче вы
увидите, как Тинтин, пятилетний мальчик, создает проблемы для своих родителей.
Тинтин - веселый мальчик и всегда занят делами. Но не все что он делает,
доставляет радость его родителям. Больше всего ему нравится играть с домашними
вещами, как например часы отца или расческа матери. После игры он не возвращает
их на место. Тинтин очень умный мальчик с достаточно четкой памятью. Он расстраивает
своих родителей тем, что никогда не возвращает вещи, взятые для игры, на
первоначальное место.
Подумать только!
Как-то утром Тинтин удалось украсть три предмета домашнего обихода. Сколькими
способами он может вернуть эти вещи так, чтобы ни один из предметов не попал на
свое прежнее место? Тинтин не хочет расстраивать своих родителей и доставлять
им неприятности. Поэтому он ничего не прячет в новых местах, а просто
переставляет предметы.
Вход. Состоит из нескольких тестов. Каждый тест представлен
натуральным числом, не большим 800 – количеством вещей, которое Тинтин взял для
игры. Каждое число находится в отдельной строке. Последняя строка содержит –1
(минус один) и не обрабатывается.
Выход. Для каждого
теста вывести количество способов, которыми Тинтин может вернуть взятые вещи.
|
Пример
входа |
Пример
выхода |
|
2 3 4 -1 |
1 2 9 |
РЕШЕНИЕ
комбинаторика,
задача о беспорядках
Анализ алгоритма
Рассмотрим формулу
включения - исключения. Пусть S – некоторое множество, P = {p1,
p2, …, pn} – свойства, которые могут иметь
элементы из S. Обозначим через S(p1 p2 … pn)
количество элементов из S, которые имеют одновременно свойства p1,
p2, …, pn. Тогда количество элементов из S,
которые не имеют ни одного свойства pi, равно
|S| - 
+ 
- … + (-1)k
+ … +
+ (-1)n
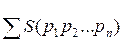
Рассмотрим в
качестве S множество всех
перестановок чисел от 1 до n. Тогда pi – это свойство
перестановки оставлять на месте элемент i. Беспорядком называется такая
перестановка, в которой не существует ни одного свойства pi.
Таким образом S(
) = (n – k)!, а количество перестановок чисел
от 1 до n, которые оставляют k элементов на месте, равно 
. Отсюда следует, что количество перестановок - беспорядков
равно
n! - 
(n - 1)! + 
(n - 2)! + … + (-1)k 
(n - k)! + … (-1)n =
n! (1 - 1 + 
- 
+ … + 
+ … + 
) 
Пример. Пусть имеется n = 3 элемента. Тогда количество перестановок, у которых на первом
месте стоит 1, равно 2: это перестановки (1, 2, 3) и (1, 3, 2). Количество
перестановок, у которых на втором месте стоит 2, равно 2: это перестановки (1,
2, 3) и (3, 2, 1). Тройка на третьем месте стоит в перестановках (1, 2, 3) и
(2, 1, 3). Таким образом, S(p1)
= S(p2) = S(p3) = 2.
Перестановкой, в
которой на первом месте стоит 1, а на втором 2, является (1, 2, 3). То есть S(p1p2) = 1. Аналогично S(p2p3)
= S(p1p3) = 1. Заметим, что S(p1p2 p3) = 1. Таким образом, для
трех вещей количество перестановок – беспорядков равно
3! – 2 – 2 – 2 +
1 + 1 + 1 – 1 = 2
Этими двумя
беспорядками будут перестановки (2, 3, 1) и (3, 1, 2).
Теорема. Обозначим через
f(n) количество перестановок – беспорядков для множества {1, 2, …, n}.
Тогда имеет место рекуррентное соотношение (1):
f(2n) = 2n
* f(2n – 1) + 1,
f(2n + 1)
= (2n + 1) * f(2n) – 1,
f(1) = 0
Доказательство. Для четного
аргумента имеем:
f(2n) =
(2n)! (1 – 1 + – + … + 
) =
(2n)! (1 –
1 + – + … – 
) + 1 =
(2n) ((2n
– 1)! (1 – 1 + – + … – )) + 1 = (2n) f(2n – 1) + 1.
Аналогично
получаем для нечетного аргумента:
f(2n + 1)
= (2n + 1)! (1 – 1 + – + … – 
) =
(2n +1)!
(1 – 1 + – + … + ) – 1 =
(2n + 1)
((2n)! (1 – 1 + – + … + )) – 1 = (2n + 1) f(2n) – 1.
Задача решается
вычислением всех значений f(n) для n £ 800.
Следствие. Количество беспорядков f(n)
можно также записать в виде
f(n) = n * f(n – 1) + (-1)n
Также имеет
место рекуррентность:
f(n) = (n – 1) * (f(n – 1) + f(n – 2))
Второе решение
Выберем число,
которое будет стоять на 1-ой позиции. Это может быть любое число, кроме единицы
(имеем (n – 1) вариантов для первого числа). Пусть
число, которое стоит на первой позиции, равно k. Рассмотрим число,
которое будет стоять на k-й позиции. Есть два варианта:
а) Если на k-й
позиции стоит 1, то поменяли числа 1 и k местами, и оставшиеся (n – 2) числа необходимо расставить на оставшиеся (n – 2) позиции, то есть задача сведена к подзадаче для (n – 2) чисел, так как удалили два числа вместе с
соответствующими позициями.
б) Допустим, что
на k-й позиции стоит не 1, а какое-то другое число. Рассмотрим
подзадачу, в которой расставим на позиции со 2-й по n-ую числа 1, 2, ...
k – 1, k + 1, ..., n, то есть все числа кроме k, причем
число 1 стоит не на позиции k. Эта подзадача не аналогична исходной,
т.к. множество номеров позиций не совпадает с множеством чисел, которые мы
расставляем. Но мы можем в этой подзадаче заменить число 1 на число k, и
при этом условие задачи не нарушится, потому что знаем, что число 1 не стоит на
k-й позиции, как было оговорено раньше. Таким образом, если заменить в
этой подзадаче число 1 на число k, то получаем исходную задачу, но для (n – 1) чисел. Мы имеем право сделать такую замену, т.к. в этой
подзадаче не было 1-й позиции (т.е. после замены не появятся новые варианты
перестановки), и заменяемое число не стояло на k-й позиции ни в одной из
перестановок (то есть замена не приведет к тому, что некоторые перестановки
перестанут удовлетворять условию задачи).
Пусть ответом
задачи будет f(n). Есть (n – 1) вариантов
выбора числа для 1-й позиции. Пусть это число k. Если число 1 стоит на k-й
позиции, то оставшиеся числа можно расставить f(n – 2) способами. Если число 1 стоит не на k-й позиции,
то количество расстановок чисел {1, 2, ..., k – 1, k + 1, ..., n}
на позициях 2...n будет равняться f(n – 1). Таким образом, имеем рекуррентность (2):
f(n) = (n – 1) * (f(n – 1) + f(n – 2)),
f(1) = 0, f(2) =
1
Пример
Вычислим
значения f(i), используя формулу и рекуррентное
соотношение.
|
рекуррентность
(1) |
формула |
|
f(2) = 2 * f(1) + 1 = 1 |
f(2) = 2! (1 –
1 + |
|
f(3) = 3 *
f(2) – 1 = 3 – 1 = 2 |
f(3) = 3! (1 –
1 + |
|
f(4) = 4 *
f(3) + 1 = 8 + 1 = 9 |
f(4) = 4! (1 –
1 + 12 – 4 + 1 = 9 |
) = 3 – 1 = 2
) =|
рекуррентность
(2) |
|
f(3) = 2 * (
f(1) + f(2)) = 2 * (0 + 1) = 2 |
|
f(4) = 3 * (
f(2) + f(3)) = 3 * (1 + 2) = 9 |
|
f(5) = 4 * (
f(3) + f(4)) = 4 * (2 + 9) = 44 |
Реализация алгоритма
В массиве
p[801][MAX], MAX = 2000 будем хранить значения f(n) (p[n] = f(n)).
pt[i] будет содержать количество цифр в числе f(i), m – рабочий массив.
#define MAX 2000
int m[MAX];
int p[801][MAX], pt[MAX];
Функция mult(int n) будет пересчитывать значение f(n) в
соответствии с приведенным выше рекуррентным соотношением (1).
void mult(int
n)
{
int i, carry,
temp;
int res[MAX];
carry = 0;
for(i = 0; i
<= ptr; i++)
{
temp = (carry+m[i]*n);
res[i] = temp % 10;
carry = temp / 10;
}
while(carry
> 0)
{
res[++ptr] = carry % 10;
carry /= 10;
}
memcpy(m,res,sizeof(res));
if (n % 2)
{
i = 0; while(!m[i])
{m[i] = 9; i++;}; m[i]--;
} else
{
i = 0; while(m[i]
== 9) {m[i] = 0; i++;}; m[i]++;
}
}
Основная часть
программы. Для каждого i (2 £ i £ 800) вычисляем значение f(i) в массиве m и
сохраняем его в ячейке p[i].
memset(m,0,sizeof(m)); ptr = 0;
for(i = 2; i <= 800; i++)
{
mult(i);
memcpy(p[i],m,sizeof(m));
pt[i] = ptr;
}
Для каждого
входного значения n выводим содержимое p[n].
while (scanf("%d",&n),n!=-1)
{
if (n == 1)
printf("0"); else
for(i =
pt[n]; i >= 0; i--) printf("%d",p[n][i]);printf("\n");
}